Special Theory of Relativity

In the Special Theory of Relativity, published in his so-called “miraculous year” of 1905, Einstein had the audacity to turn the question around and ask: what must happen to our common notions of space and time so that when the distance light travels in a given time is measured, the answer is always 300,000 km/s? For example, if a spaceship fires a laser beam at a piece of space debris flying towards it at half the speed of light, the laser beam still travels at exactly the speed of light, not at one-and-a-half times the speed of light. He began to realize that either the measurement of the distance must be smaller than expected, or the time taken must be greater than expected, or both.

In fact, Einstein realized, the answer is both: space “contracts” and time “dilates” (or slows). Some of the motion through space can be thought of as being "diverted" into motion through time (and vice versa), in much the same way as a car traveling north-west diverts some of its northwards motion towards the west. Thus, the dimensions of space and time affect each other, and both space and time are therefore relative concepts, with only the unvarying speed of light providing the bedrock on which the universe is built. This revolutionary idea flew in the face of the long-held notion of simultaneity (the idea that events that appear to happen at the same time for one person should appear to happen at the same time for everyone in the universe) and suggested that it was impossible to say in an absolute sense whether two events occurred at the same time if those events were separated in space.

(Click for a larger version) At relativistic speeds, space “contracts” and time “dilates” (Source: Time Travel Research Center: http://www.zamandayolculuk.com/cetinbal/ HTMLdosya1/RelativityFile.htm)

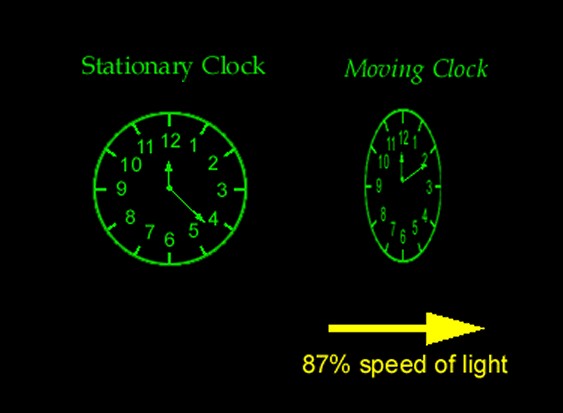
In a nutshell, the Special Theory of Relativity tells us that a moving object measures shorter in its direction of motion as its velocity increases until, at the speed of light, it disappears. It also tells us that moving clocks run more slowly as their velocity increases until, at the speed of light, they stop running altogether. In fact, it also tells us (as we will see in subsequent sections) that the mass of a moving object measures more as its velocity increases until, at the speed of light, it becomes infinite.

Thus, one person’s interval of space is not the same as another person’s, and time runs at different rates for different observers traveling at different speeds. To some extent, the faster you go, the slower you age and the slimmer you are! The reason this is not obvious in everyday situations is that the differences at everyday speeds are infinitesimally small, and only really become apparent at speeds approaching that of light itself (“relativistic” speeds). The closer the speed of an objects approaches to the speed of light, the more warped lengths and time intervals become.

The amount of length contraction and time dilation is given by the Lorentz factor, named after the Dutch physicist Hendrik Lorentz, who had been exploring such transformation equations since as early as 1895, long before Einstein began his work (indeed some would claim that Lorentz and Henri Poincaré between them anticipated almost everything in Einstein's Special Theory of Relativity). The Lorentz factor, γ (gamma) is given by the equation γ ≡ , so that the effect increases exponentially as the object's velocity v approaches the speed of light c. Thus, the calculations show that at 25% of the speed of light, the effect is just 1.03 (a mere 3% slowing of time or contraction of length); at 50% of the speed of light, it is just 1.15; at 99% of the speed of light, time is slowed by a factor of about 7; and at 99.999, the factor is 224. So, if it were possible to travel in a spaceship at, say, 99.5% of the speed of light, a hypothetical observer looking in would see the clock moving about 10 times slower than normal and the astronaut inside moving in slow-motion, as though through treacle.

A couple of real-life examples may help to make the effects of special relativity clearer. Experiments have been carried out where two identical super-accurate atomic clocks were synchronized, and then one was flown around the world on an airplane while the other stayed at home. The clock which traveled recorded marginally less passage of time than the other (as predicted by the theory), although the difference was of course minimal due to the relatively slow speeds involved. Our fastest military airplanes can only travel at about 1/300,000 of the of the speed of light, so the time dilation effect γ is only about a ten-thousandth of 1%.

At very high speeds, however, the effect is much more noticeable. Experiments have demonstrated that an ultra-short-lived muon particle, which habitually travels at 99.92% of the speed of light, actually lives about 25 times longer and travels about 25 times further than it theoretically should. Particles traveling at speeds up to 99.99% the speed of light in the CERN particle accelerator in Switzerland experience the same kind of relativity-induced time travel, experiencing a γ factor of around 5,000, allowing the artificial persistence of even shorter-lived particles such as phi mesons.

So, traveling at close to the speed of light would theoretically allow time travel into the future, as time slows down for the speeding object in order to "protect" the cosmic speed limit of the speed of light. A corollary of all this is that, if it were possible to exceed the speed of light, then it would also be possible to go back in time, which raises the possibility of time-travel paradoxes (where a person goes back in time and interferes in their own past or kills their own grandparents, etc), although some scientists believe that some as yet undiscovered law of physics may intervene to prevent such paradoxes. Actually, special relativity does not specifically forbid the existence of particles that travel faster than light, and there is a hypothetical sub-atomic particle called a tachyon, which would indeed spend its entire life traveling faster than the speed of light, but it is currently still hypothetical.

(Click for a larger version) In the "twins effect" (or paradox), a space traveler returns to Earth younger than his twin (Source: The Reference Frame: http://motls.blogspot.com/ 2007/02/resolving-einsteins-twin-paradox.html)

Another phenomenon associated with the dilation of time is the so-called “twins effect” (sometimes referred to as the “twins paradox”), where an astronaut returns from a near-light speed voyage in space to find his stay-at-home twin many years older than him (as traveling at relativistic high speeds has allowed him to experience only one year of time while ten years have elapsed on Earth). This is sometimes considered a paradox in that each twin sees the other twin as traveling, and so, it is argued, each should see the other aging more slowly. But in fact this is based on a misunderstanding of relativity, because in reality only one twin experiences acceleration and deceleration, and so only one twin ages less.

An equivalent paradox concerning the related phenomenon of length contraction is often referred to as the "tunnel paradox", whereby a hypothetical train approaching a tunnel at near-light speed sees the tunnel as much shorter than it really is, whereas someone in the tunnel sees the approaching train as short.

Essentially, then, the Special Theory of Relativity can be boiled down to its two main postulates: firstly, that physical laws have the same mathematical form when expressed in any inertial system (so that all motion, and the forces that result from it, is relative); and secondly that the speed of light is independent of the motion of its source and of the observer, and so it is NOT relative to anything else and will always have the same value when measured by observers moving with constant velocity with respect to each other. Not such a scary proposition at first glance, perhaps, but it does lead to some rather interesting implications, which we will begin to consider in subsequent sections.