Curved Space

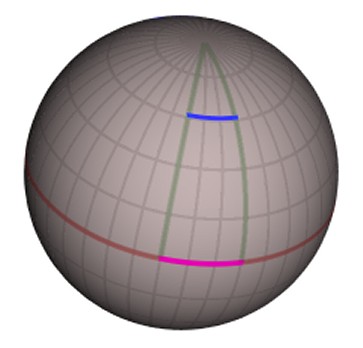
If we imagine again the astronaut in his accelerating spaceship cabin from the previous section, and imagine him pointing a laser horizontally across the cabin, the upward motion of the spacecraft would result in the path of the laser appearing to curve (very) slightly downwards as it crosses the cabin. Now, we know that light always takes the shortest path between two points, which we usually think of as a straight line. However, a straight line is only the shortest distance between two points on a flat surface. On a curved surface, the shortest distance between two points is actually a curve, technically known as a geodesic, which we can perhaps visualize when we think, for example, of a plane flying the shortest route between London and New York which, as travelers will know, follows a "great circle" path over Newfoundland rather than what appears to be a more direct straight line on a flat map.

The only possible interpretation of the curving laser beam, then, is that the space inside the cabin is in some way curved. If we combine this concept with Einstein's principle of equivalence, then it would appear that light in the presence of gravity follows a curved trajectory, or, put in another way, gravity bends the path of light. In fact, it turns out that gravity is nothing more than curved space, or, more specifically, the curvature or warpage of four-dimensional space-time.

(Click for a larger version) A geodesic is the shortest path between two points in curved space (Source: Wikipedia: http://en.wikipedia.org/wiki/ Introduction_to_general_relativity)

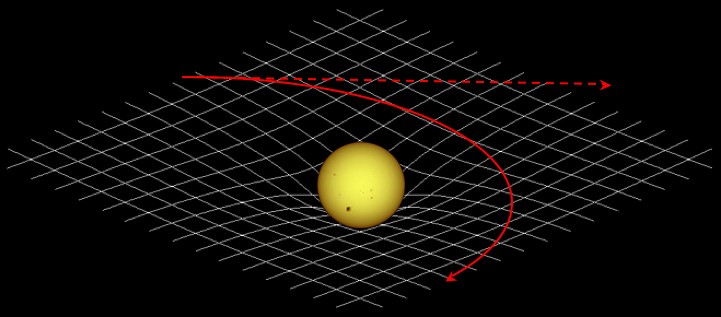
A simple analogy might help us to understand this notoriously hard-to-visualize concept. If a group of ants spend their entire lives on the essentially 2-dimensional surface of a trampoline, and a heavy weight like a bowling ball is placed in the middle of the trampoline, the ants will find their paths mysteriously bent towards the bowl-like depression in the trampoline. The ants might explain it by saying that the weight is exerting a force of attraction on them, but, from the elevated point of view of the third dimension, it is clear that the ants are merely following the curve of the trampoline and that no actual force is acting on them.

An even better visual analogy might be if a marble is rolled along the trampoline surface. It might roll straight past the bowling ball, or it might be deflected a little (or a lot) as it follows the dip but then "escapes" (similar to the idea of using gravity to deflect or brake or slingshot a spaceship around a planet's orbit). Or, if the marble comes too close, then it might be drawn inexorably into the depression of the bowling ball, rolling in ever-decreasing circles until it joins the ball in its hollow.

(Click for a larger version) Gravity causes space-time to curve around massive objects (Source: Time Travel Research Center: http://www.zamandayolculuk.com/cetinbal/ HTMLdosya1/RelativityFile.htm)

The path of the Earth as it travels through space is constantly bent towards the Sun in this way, so much so that the planet traces out a nearly circular orbit. From the God-like perspective of the fourth dimension, however, it can be seen that there is no actual force being exerted on the Earth, merely that the Sun has created a valley-like depression in four-dimensional space, and the Earth is just following the shortest path along a geodesic through the curved space-time (just as the ants were in three-dimensional space).

The Earth, then, is actually in free fall around the Sun and so we do not feel the Sun's gravity on earth, just as astronauts on the International Space Station in free fall around the Earth do not feel the Earth's gravity. Thus, although free fall is usually defined as motion with no acceleration other than that provided by gravity, what it is really is just a body traveling along the straightest possible path through space-time. We only "feel" gravity on the Earth when our natural motion of free fall towards the center of the Earth is thwarted by the ground, an inertial force similar to centrifugal force, as was mentioned in the previous section.

This may at first seem counter-intuitive. We are used to the Newtonian idea that, when we throw a ball straight up in the air, for example, a graph of its height versus time traces out a parabola curve. Under relativity, however, we must recognize that a massive body like the Earth actually curves the coordinate system itself, so that rather than following a curved path in a flat (Cartesian) coordinate system, the ball actually follows a minimum-distance path, or geodesic, in a curved coordinate system, returning to the thrower's hand at a later time because the geodesic leads it there.