E = mc²

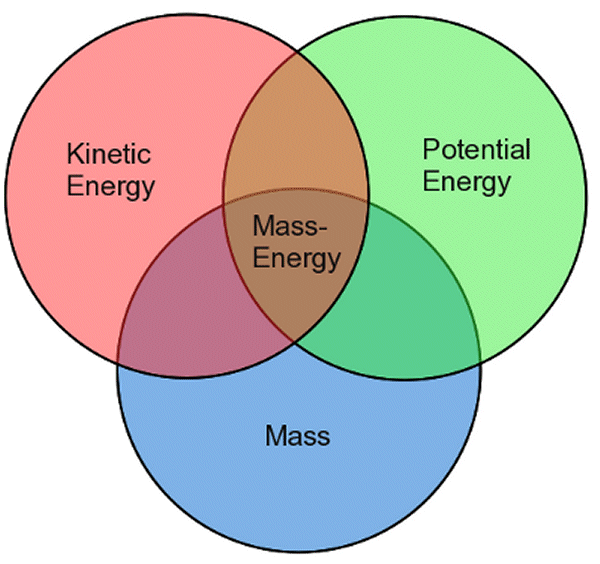
As the Sun pumps out energy and light, it actually also loses some of its mass, although very slowly (less than 0.1% since its birth). As a comet’s path passes near to the Sun, a tail of glowing gases billows out away from the Sun. Both of these examples suggest that the energy (photons) leaving the Sun actually weighs something, actually has mass, even if very little. Although photons of sunlight have no intrinsic mass (otherwise, as we will see, they would be unable to travel at the speed of light), they must have an “effective mass” by virtue of their energy in order to be able to push a comet’s tail.

If a body with mass is pushed ever closer to the speed of light, the body would have to become harder and harder to push, so that its speed never actually reached or exceeded the speed of light, which we know to be the de facto maximum speed. In fact, by extension, if a material body were ever to reach the speed of light it would effectively have to have acquired an infinite mass. As a body approaches the speed of light, then, the energy put into pushing the body clearly cannot be used to increase its velocity and must therefore go somewhere else.

(Click for a larger version) Mass-Energy Venn diagram (Source: Arachnoid: http://www.arachnoid.com/gravity/ index.html)

The Law of Conservation of Energy dictates that energy can neither be created nor destroyed, only transformed from one form to another. It follows, then, that if the energy pushing the body is being converted into additional mass, then mass itself is just another form of energy, and, vice versa, energy (energy of any sort, not just light, including sound energy, electrical energy, energy of motion, etc) therefore has an effective mass.

This connection between energy and mass, known as mass-energy equivalence, was immortalized in Einstein’s equation E = mc², where E stands for energy, m stands for mass and c is a constant (which happens to be equal to the speed of light). Actually, E = mc² is just the simplest case scenario, that for a body or mass at rest. For a body in motion, with a velocity v, the equation becomes E = . We have already seen that the Lorentz factor γ ≡ , so we can therefore also say that E = γm_oc² (where m_o is the rest mass of the object). As can perhaps be reasonably easily deduced from these equations, as the velocity (v) approaches the speed of light (c), energy (E) approaches infinity, indicating that the body would in fact require an infinite amount of energy to accelerate to the speed of light. We can also see how (as mentioned in a previous section) the mass of a moving object becomes greater and greater as its velocity increases until, at the speed of light, it becomes infinite.

Like other aspects of relativity, though, the effects are very hard to observe in the everyday world. Your cup of coffee actually does weight more when you have added heat energy to it, but by such an infinitesimal amount as not to be noticeable or even measurable. Likewise, when a piece of coal is burned, mass-energy is converted to heat energy, and the total products of burning (ash, gases, etc) would in fact weigh slightly less than the original coal.

To take another example, although four atoms of hydrogen can be used to produce one atom of helium, as occurs during nuclear fusion in the heart of the Sun or in a hydrogen bomb, the atom of helium actually weighs 0.8% less than four hydrogen atoms, the balance being converted into heat energy. This tiny "weight" of heat energy, however, represents about a million times as much energy as an equivalent weight of coal could produce, partly due to the prodigious strength of the strong nuclear force which holds the nucleus of an atom together.

(Click for a larger version) The Large Hadron Collider at CERN, Switzerland, uses extremely high energy to create particles of mass (Source: Berkeley Lab: http://www.lbl.gov/publicinfo/newscenter/ features/08/06/12/AFRD-LHC.html)

The same principle applies in reverse in particle colliders like that at CERN, the European center for particle physics in Switzerland. In a particle collider, sub-atomic particles are accelerated to huge speeds and then crashed together, in the hope of creating new exotic particles of matter out of the massive energy discharge which results. The prodigious amounts of energy required to cause particles to literally pop out of thin air in this way is an indication of just how much energy is encapsulated within mass.

In fact, mass is the most concentrated form of energy known. When one considers the equation E = mc², the term c stands for the speed of light (300,000 kilometers per second) and this term is squared, which results in a very large number indeed. Thus, it may come as no surprise that applying the equation to one kilogram of matter shows that it contains 9 x 10¹⁶ joules of energy, enough to lift the entire population of the Earth into space!

However, converting matter into energy is not easy. The nuclear processes in the Sun and in a hydrogen bomb liberate barely 1% of the energy locked up in matter. A black hole spinning at its maximum possible rate is much more efficient, though, and as matter swirls into a black hole, it liberates energy (as heat and light) equivalent to 43% of the mass of the matter. This is one reason why scientists believe that the huge energy output of quasars can only be generated by a supermassive black hole at its heart.

In fact, the only process that converts mass into energy with 100% efficiency is the meeting of matter and antimatter. Unfortunately, our universe appears to contain hardly any antimatter (which remains something of a puzzle because, when antimatter is created in the laboratory, its birth is always accompanied by an equal amount of matter), and scientists have only succeeded in producing less than a billionth of a gram. The production of antimatter is fraught with expense and difficulty (especially given that it tends to annihilate as soon as it meets ordinary matter!), but if an efficient method of production could be found one day, we would have at our command the most powerful energy source imaginable (like the antimatter drive of fictional Star Trek).