Quantum Tunneling and the Uncertainty Principle

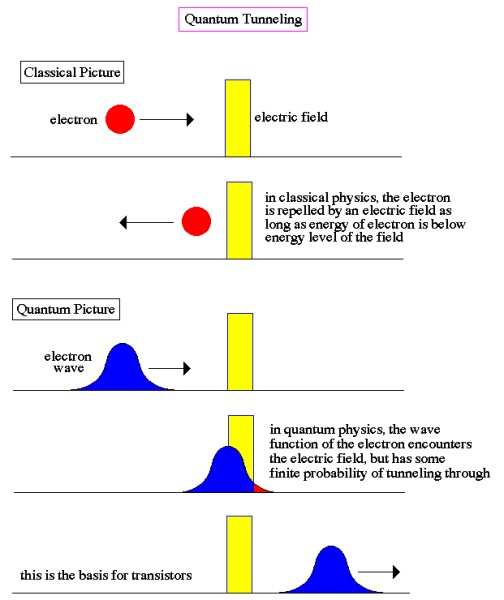
One of the consequences of light having a wave-like aspect is exemplified by its apparent ability to jump gaps. For instance, light penetrating through a block of glass at a shallow angle is effectively trapped within the glass by the barrier of air at the far side, unless a second glass block is placed close to it (but not touching). Because of the spread-out nature of the wave, some of it penetrates the air barrier and if encounters more glass beyond it can continue, thus apparently jumping the air gap and escaping its prison.

A similar thing happens at the sub-atomic scale, when alpha particles try to escape from unstable nuclei during radioactive decay. The particles are effectively held in the nucleus by the nuclear forces and, in principle, should not be able to escape. However, escape they do, using a process known as quantum tunneling, which makes use of the wave-like aspect of the particles, but also of a more general phenomenon known as "uncertainty" (which we will look at in more detail below).

Due to the wave-like aspect of particles, and the ability to describe an object by means of a probability wave, as we have seen, quantum physics predicts that there is a finite probability that an object trapped behind a barrier (without the energy to overcome the barrier) may at times appear on the other side of the barrier, without actually overcoming it or breaking it down. For instance, if an electron approaches an electric field and is repelled by it, there is nevertheless some probability, however small, that it will find itself on the other side of the field (see image below).

(Click for a larger version) Quantum tunneling through a barrier (Source: U. of Oregon Lectures: http://abyss.uoregon.edu/%7Ejs/ast123/lectures/lec06.html)

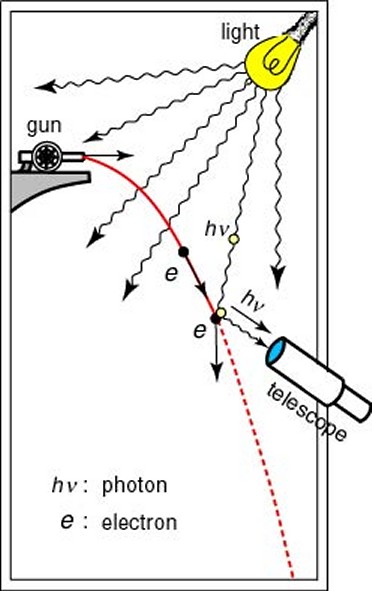
This possibility of being detected on the other side of a barrier has become known as tunneling, although there is certainly no actual physical digging going on. It can perhaps be best visualized by imagining a broad wave approaching, and then slightly overlapping, a barrier. Although the main part of the wave may never penetrate the barrier, a small part of it does, allowing for the possibility of the particle which is generating the wave suddenly being located on the other side of the barrier.

The uncertainty principle was first recognized by the German physicist Werner Heisenberg in 1926 as a corollary of the wave-particle duality of nature. He realized that it was impossible to observe a sub-atomic particle like an electron with a standard optical microscope, no matter how powerful, because an electron is smaller than the wavelength of visible light. He conceived of an imaginary microscope which used gamma rays (which have a wavelength much smaller than an electron) rather than visible light. But, because gamma rays are so much more energetic than visible light, they would have the effect of changing the speed and direction of the electron in an unpredictable and uncontrollable way. So, in solving one part of the problem, another problem is necessarily created.

In fact, through his famous “microscope” thought experiment, he realized that a similar thing was happening to some extent even within a standard optical microscope. To measure the position and velocity of a particle, a light can be shone on it, and then the reflection detected. On a macroscopic scale this method works fine, but on sub-atomic scales the photons of light that hit the sub-atomic particle will cause it to move significantly. So, although the position may have been measured accurately, the velocity of the particle will have been altered, and, by learning the position, any information previously known about the velocity has been rendered useless. In other words, the very act of observation affects the observed.

(Click for a larger version) Heisenberg's microscope thought experiment to illustrate the effects of the uncertainty principle (Original Source N/A: kutl.kyushu-u.ac.jp/ seminar/MicroWorld2_E/2Part1_E/ 2P14_E/Heisenberg_QM_E.htm)

Heisenberg realized, then, that the values of certain pairs of variables cannot BOTH be known exactly, so that the more precisely one variable is known, the less precisely the other can be known. If the speed (or, more strictly, the momentum) of a particle is known exactly, then its location must be uncertain; conversely, the more certainly its location is known, the less certain is the particle’s speed (or momentum). Likewise, if the energy state of a particle is known with certainty, then it can not be determined how long it will remain in that state (and vice versa). In slightly more mathematical terms, he showed that the uncertainty in the position of a particle times the uncertainty in its velocity times its mass can never be smaller than a certain quantity, known as the Planck constant.

With the advent of the uncertainty principle, then, particles could no longer be said to have separate, well-defined positions and velocities, but only a “quantum state”, a combination of position and velocity. If it is not possible to know the values of all of the properties of the system at the same time, then those properties that are not known with precision must be described by probabilities. The principle effectively overturned in one fell swoop the whole doctrine of scientific determinism which had been implicitly assumed since Newton and Laplace in the 17th Century, and redefined the task of physics as the discovery of laws that will allow us to predict events UP TO THE LIMITS set by the uncertainty principle.

In a way, the uncertainty principle exists to protect quantum theory, in that if the properties of atoms and particles could be known with certainty, then they would decohere and their wave behavior and their ability to interfere would thereby be destroyed. There is therefore a built-in limit to our knowledge of the microscopic world, and nature does not permit us to measure precisely all we would like to measure. However, it should be noted that this is not due to imprecise measurements in practice (technology is advanced enough to hypothetically yield correct measurements); rather, the blurring of the measurable quantities of a particle (mass, velocity and position) is a fundamental property of nature itself, and does not depend on the type of particle or the method of measurement.

(Click for a larger version) An energy-losing electron should fall into the nucleus (Source: TutorVista: http://www.tutorvista.com/content/chemistry/ chemistry-i/atom/atomic-models.php)

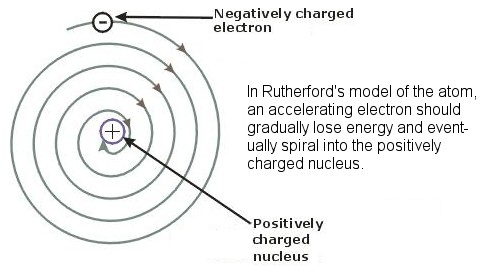
Returning, then, to the earlier question (introduced back in the section on the Early Developments in Atomic Theory) of why orbiting electrons do not lose energy and spiral into the nucleus of an atom, it is the uncertainty principle that prevents electrons from approaching the nucleus too closely. If an electron gets too close then its location in space would be very precisely known, and its velocity would therefore be very uncertain and it could acquire enormous speed, enough to ensure that it did not stay confined in the nucleus.

In the same way, the uncertainty principle explains how an alpha particle is able to escape the nucleus of a radioactive atom. Trapped in the nucleus, the alpha particle is very localized in space, and its position is pinned down with great accuracy. In that case, according to the uncertainty principle, its velocity must be very uncertain, possibly much greater than we would have expected, and possibly enough to escape the pull of the nucleus.

A similar situation in reverse explains how nuclear fusion is possible in the Sun, when the temperatures in the Sun are actually about a thousand times cooler than the massive temperatures which are theoretically needed to provide the incoming protons with enough energy and speed to overcome the strong repulsive electromagnetic force of the receiving hydrogen atoms. By virtue of quantum tunneling and Heisenberg’s uncertainty principle, the protons can “tunnel” through the barrier even given the apparently insufficient temperature and energy.

The uncertainty principle also explains why a typical atom is over 100,000 times bigger than the nucleus at its center. Strictly speaking, the uncertainty principle holds that it is a particle’s position and its momentum (its mass times its velocity, as opposed to just its velocity) which cannot be simultaneously be known with certainty. Because an electron is about 2,000 times less massive than the protons in a nucleus, and because the repulsive electromagnetic force it is subject to is about 50 times weaker than the strong nuclear force in the nucleus, these two factors together result in the need for about 100,000 times as much space for the electron to move around in.

(Click for a larger version) Virtual electron-positron pairs appearing at random near an electron (Source: Wikipedia: http://en.wikipedia.org/wiki/Electron)

In fact, the uncertainty principle can be reformulated in yet another way to say that it is impossible to simultaneously measure the energy of a particle and the interval of time for which it has been in existence. Over a very tiny interval of time, there can therefore be a large uncertainty in the energy content of a particular location, and energy or even pairs of fundamental particles (known as "virtual particles", because they exist for such a short time that they are not considered part of everyday reality) could even appear out of nothing in the apparently empty vacuum of space and exist for a split-second before disappearing again. The more energy that is put into a vacuum, the more particles causelessly pop out of it. It appears, then, that there is no such thing as empty space.

Such a phenomenon (particles constantly popping in and out of existence), unlikely though it may sound, is well documented and has actually been indirectly observed through observations of the changing energy of existing electrons which are buffeted by such appearances and disappearances. In effect, the energy needed to create these virtual particles can be "borrowed" from the vacuum for a period of time, but the net energy from the reaction is still zero. Because overall they cancel each other out, they cannot be said to even exist in the classical world, nor to break any of the laws of classical physics.