Spin and the Pauli Exclusion Principle

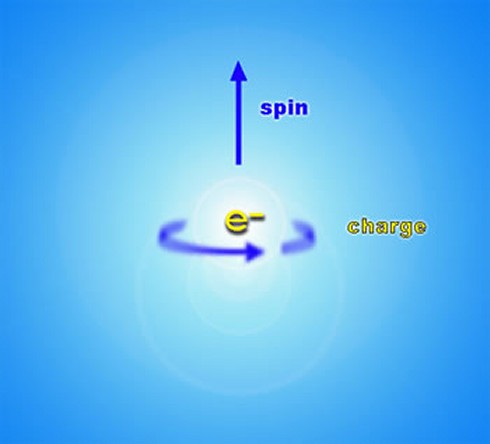
To return to the property of spin of fundamental particles, mentioned briefly in the previous section, spin can perhaps be most easily thought of as a rotation of particles around their own axis, although this is in fact something of a simplification, and in reality it is impossible to tell whether something as small as an electron is spinning at all. In general, though, spin obeys the same mathematical laws of angular momentum as do spinning objects in classical physics (such as the Earth, for instance), and there are really only two important aspects to consider: the speed of rotation and the direction of the axis it rotates about (referred to as “up” and “down”).

When spin was first discovered in 1922 by Otto Stern and Walther Gerlach, however, their experiments indicated that the intrinsic angular momentum, or spin, of a particle such as an electron was quantized i.e. it could only take certain discrete values. The spin of composite particles (such as protons, neutrons and atomic nuclei) is just the sum of the spins and orbital angular momentum of the constituent particles, and is therefore subject to the same quantization conditions. Spin is therefore a completely quantum mechanical property of a particle, and cannot be explained in any way by classical physics.

(Click for a larger version) Artist's representation of the spin and charge of an electron (Source: Berkeley Lab: http://www.lbl.gov/Science-Articles/ Archive/sabl/2006/Jan/02-spin-drag.html)

Now, it turns out that there are two sub-categories of particles: those with “integer” spin, which are known as bosons, and which include photons, gluons, W and Z bosons and hypothetical gravitons; and those with “half-integer spin”, which are known as fermions, and which include electrons, neutrinos, muons, and the quarks which make up composite particles like protons and neutrons. Another way of describing the difference between bosons and fermions is that bosons have symmetric wave functions while fermions have antisymmetric wave functions. The concept of a particle with half-integer spin is just another example of the apparently counter-intuitive nature of sub-atomic particles: crudely speaking, a fermion such as an electron has to spin around TWICE before it presents the same face as before.

The significance of this distinction for quantum theory is that the probability waves of bosons “flip” or invert before they interfere with each other, which effectively leads to their more “gregarious” nature, which in turn can lead to collective behavior like that of lasers, superfluids and superconductors. Fermions, however, do not flip their probability waves, which, among other implications, leads to their “unsociable” nature. Thus, the spins of particles have to be added together very carefully using special rules for addition of angular momentum in quantum mechanics.

This discussion of the property of spin leads us to one of the most important principles in quantum physics, the Pauli exclusion principle (formulated by Wolfgang Pauli in 1925), which states that no two identical fermions may occupy the same quantum state simultaneously (although two electrons, for example, may acquire opposite spin in order to differentiate their quantum states). Another way of stating the principle is that no two fermions in a quantum system can have the same values of all four quantum numbers at any given time. This principle effectively explains the continued existence of very high-density white dwarf stars, but also the very existence of different types of atoms in the universe and the large-scale stability and bulk of matter.

(Click for a larger version) Electron shell diagram for the element uranium (using the Bohr model of the atom) (Source: Wikipedia: http://en.wikipedia.org/wiki/Wikipedia: Picture_peer_review/Electron_shells)

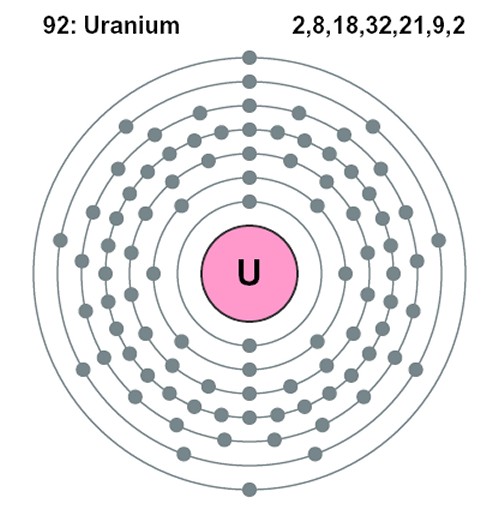
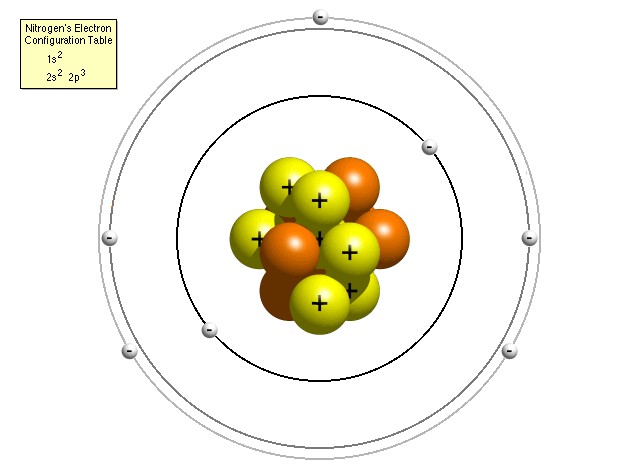
To understand why, it is necessary to know that, according to the Bohr model of the atom, electrons in an atom (which exist in the same quantity as the number of protons in the nucleus of the particular atom, so that the overall electric charge is zero) are constrained to occupy certain discrete orbital positions or “shells” around the nucleus. The closer electrons are to the nucleus, the more strongly the electric force is pulling them in and the more energy would be required to free it from the clutches of the nucleus (or, looked at another way, the more energy of its own an electron has, the less additional energy it needs in order to escape). The innermost shell can accommodate just two electrons, one with spin “up” and one with spin “down” in order to differentiate their quantum states. The next shell out, in a higher energy level, can accommodate a further eight, the next a further eighteen and the next thirty-two.

Actually, more recent research has yielded a more accurate “refined” Bohr model of the atom with each energy level composed of a certain number of sub-shells (named s, p, d and f) which can each hold only a certain number of electrons. For instance, the s sub-shell can only hold 2 electrons, the p sub-shell can hold 6, the d sub-shell can hold 10 and the f sub-shell can hold 14. The number of available sub-shells increases as the energy level increases, so that successive shells can hold a total of 2, 8, 18 and 32 electrons.

(Click for a larger version) Depiction of an atom of nitrogen (using the refined Bohr model) (Source: Jefferson Lab: http://education.jlab.org/ qa/atom_model.html)

It is the Pauli exclusion principle which dictates this arrangement and effectively forces electrons to “take up space” in the atom through this arrangement of shells. By recognizing that no two electrons may occupy the same quantum state simultaneously, it effectively stops electrons from "piling up" on top of each other, thus explaining why matter occupies space exclusively for itself and does not allow other material objects to pass through it, while at the same time allowing light and radiation to pass.

It also explains the existence of the different atoms in the periodic table of elements and the sheer variety of the universe around us. For example, when an atom gains a new electron, it always goes into the lowest energy state available (i.e. the outermost shell). Two atoms with “closed” shells find they cannot form a chemical bond with each other because the electrons in one atom find no available quantum states in the other which it can occupy. So, the arrangement of electrons, particularly of the electrons in the outermost shell, also affects the chemical properties of an element and how atoms are able to bond and combine with other atoms (the basis of chemistry), and therefore the way in which molecules interact to form gases, liquids or solids, and how they aggregate themselves in living organisms.

Another effect of the Pauli exclusion principle is that, if two identical particles are forced (for instance, by an extremely strong gravitational force) to try to have the same quantum numbers, they will respond with a repelling outward force, known as "degeneracy pressure" or "Pauli repulsion". A type of star called a degenerate white dwarf is held up entirely by this force.

The Pauli exclusion principle is one of the most important principles in quantum physics, largely because the three types of particles from which ordinary matter is made (electrons, protons and neutrons) are all subject to it, so that all material particles exhibit space-occupying behavior. Interestingly, though, the principle is not enforced by any physical force understood by mainstream science. When an electron enters an ion, it somehow mysteriously seems to "know" the quantum numbers of the electrons which are already there, and therefore which atomic orbitals it may enter, and which it may not.