Event Horizon and Accretion Disk

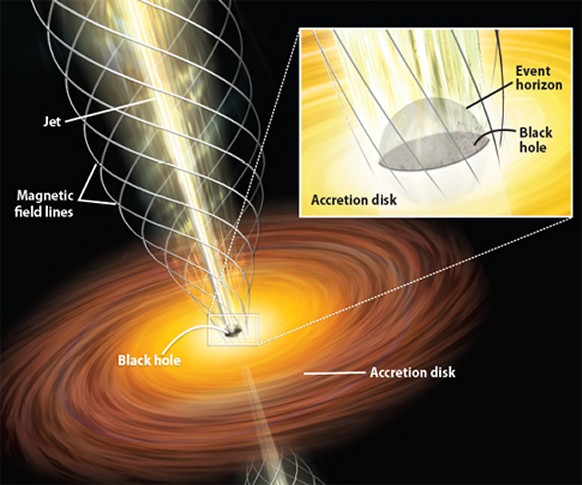
A black hole’s mass is concentrated at a single point deep in its heart, and clearly cannot be seen. The “hole” that can, in principle, be seen (although no-one has ever actually seen a black hole directly) is the region of space around the singularity where gravity is so strong that nothing, not even light, the fastest thing in the universe, can escape, and where the time dilation becomes almost infinite.

A black hole is therefore bounded by a well-defined surface or edge known as the “event horizon”, within which nothing can be seen and nothing can escape, because the necessary escape velocity would equal or exceed the speed of light (a physical impossibility). The event horizon acts like a kind of one-way membrane, similar to the "point-of-no-return" a boat experiences when approaching a whirlpool and reaching the point where it is no longer possible to navigate against the flow. Or, to look at it in a different way, within the event horizon, space itself is falling into the black hole at a notional speed greater than the speed of light.

(Click for a larger version) Event horizon, accretion disk and gamma ray jets of a black hole (Source: Internet Encyclopedia of Science: http://www.daviddarling.info/ encyclopedia/E/event_horizon.html - Credit & ©: Astronomy / Roen Kelly)

The event horizon of a black hole from an exploding star with a mass of several times that of our own Sun, would be perhaps a few kilometers across. However, it could then grow over time as it swallowed dust, planets, stars, even other black holes. The black hole at the center of the Milky Way, for example, is estimated to have a mass equal to about 2,500,000 suns and have an event horizon many millions of kilometers across.

Material, such as gas, dust and other stellar debris that has come close to a black hole but not quite fallen into it, forms a flattened band of spinning matter around the event horizon called the accretion disk (or disc). Although no-one has ever actually seen a black hole or even its event horizon, this accretion disk can be seen, because the spinning particles are accelerated to tremendous speeds by the huge gravity of the black hole, releasing heat and powerful x-rays and gamma rays out into the universe as they smash into each other.

These accretion disks are also known as quasars (quasi-stellar radio sources). Quasars are the oldest known bodies in the universe and (with the exception of gamma ray bursts) the most distant objects we can actually see, as well as being the brightest and most massive, outshining trillions of stars. A quasar is, then, a bright halo of matter surrounding, and being drawn into, a rotating black hole, effectively feeding it with matter. A quasar dims into a normal black hole when there is no matter around it left to eat.

A non-rotating black hole would be precisely spherical. However, a rotating black hole (created from the collapse of a rotating star) bulges out at its equator due to centripetal force. A rotating black hole is also surrounded by a region of space-time in which it is impossible to stand still, called the ergosphere. This is due to a process known as frame-dragging, whereby any rotating mass will tend to slightly "drag" along the space-time immediately surrounding it. In fact, space-time in the ergosphere is technically dragged around faster than the speed of light (relative, that is, to other regions of space-time surrounding it). It may be possible for objects in the ergosphere to escape from orbit around the black hole but, once within the ergosphere, they cannot remain stationary.

Also due to the extreme gravity around a black hole, an object in its gravitational field experiences a slowing down of time, known as gravitational time dilation, relative to observers outside the field. From the viewpoint of a distant observer an object falling into a black hole appears to slow down and fade, approaching but never quite reaching the event horizon. Finally, at a point just before it reaches the event horizon, it becomes so dim that it can no longer be seen (all due to the time dilation effect).